After spending some time reading about Arrows I decided to rebuild a home battery simulator I’ve been working on using the concepts from Functional Reactive Programming (FRP) and Arrows. I was disappointed that I was unable to build larger simulations from smaller components using my previous approach, so after reading about Arrows I was pretty optimistic about the approach.

Arrows offer a few interesting features that I thought would be useful for building simulations:

• Input tracking: allows me quickly determine which inputs are time-varying and which are constant.
• Composition: Arrows provide a way to compose smaller computations into larger ones like this (>>>) :: Arrow a => a b c → a c d → a b d.
• ArrowLoop: provides a way to create feedback loops in a controlled manner.

You can read more about Arrows in my article Generalising Monads to Arrows which summarises a paper by John Hughes. I also created a cheat sheet for Arrow combinators that I find slightly easier to navigate than Hoogle/Hackage. To learn more about ArrowLoop and arrow proc syntax I recommend A New Notation for Arrows by Ross Paterson.

In this article I’ll describe simulating a home battery with multiple control modes using Yampa, an FRP library for Haskell that uses Arrows as its core abstraction.

The Simulation

I want to build a simulation of a homes power usage. It needs to be accurate enough for me to explore different control strategies for various devices (like solar systems, batteries, hot water systmes and EV/EV charges). Furthermore, I want to be able to explore different scales of usage from a single home to a fleet of devices.

While not an overwhelming technical challenge, building a simulation that is accurate enough to be useful while remaining simple enough to be maintainable requires some nuance. Each device in a home may interact with other devices in interesting ways. For example, both a battery and an EV charger may attempt to draw power based on the total load of the home, each device is aware of the power the other is drawing without being aware of the other device directly. This leads to interesting feedback loops that must be handled carefully to avoid instability in the simulation.

Signal Functions

The Yampa libraries core abstraction is the Signal Function (SF). A signal function a function that transforms a time-varying input signal of type a into a time-varying output signal of type b.

This is represented in Haskell as SF a b. I read this as an arrow from a to b over that varies over time. More concretely, this is one of the first function we’ll look at batteryPhysics :: BatterySpec -> BatteryState -> SF PowerRequest BatteryState. It returns a behaviour that transforms a PowerRequest at a given point of time into a new BatteryState at that same point in time.

Using SF immediately made it clear that the physics of the battery could be separated from the control logic. Originally, when I tried to model batties using state machines I did not have a clear separation between the physics of the battery and the control logic. But the Arrow/Yampa framework immediately made this distinction clear.

The Battery Model

Home batteries in this simulation have two components: the physics governs how the battery state changes when charging and discharging. The control logic decides when to charge or discharge based on the power load of the home and the battery state. This distinction makes each component easier to reason about.

batteryPhysics  :: BatterySpec 
                -> BatteryState 
                -> SF PowerRequest BatteryState

-- There are multiple control modes for the battery
type ControlMode = SF (BatteryState, SiteLoad) ChargeRequest

-- Solar soak is a control mode that charges the battery with excess solar power but never discharges
solarSoakControl :: BatterySpec -> ControlMode

-- Load following is a control mode where the battery  charges on excess solar and discharges to meet load
loadFollowingControl :: BatterySpec -> ControlMode

-- Control Modes for the battery
data Control
  = Charging Power
  | Discharging Power
  | LoadFollowing
  | SolarSoak
  | Idle

-- The battery combines the physics with the various control modes and an event stream to switch between control modes
battery :: BatterySpec 
        -> BatteryState 
        -> Control
        -> SF (SiteLoad, Event Control) BatteryState

The beautiful pattern is a control mode will inspect some broader context to make a decision about how to charge or discharge the battery and pass that request to the battery physics which understand what is actually possible for the battery to do.

The implementations for the control modes and battery physics are straightforward, and combine independently of each other as more accuracy is required. The implementation of battery was more difficult, and there are a few reasons for this:

1. The battery needs to switch behaviours based on the Event stream in its input.
2. Determining how to construct a new SF when switching control modes requires access to the current battery state.
3. Composing the physics with the control requires feedback loops.
4. There are some tricks you need to know to use Yampa effectively.

Control Switching

Yampa has great combinators for switching between signal functions. Unfortunately, it’s a bit hard to understand what each one of them does. There’s are diagrams here, descriptions of the diagrams on Redit, and descriptions in the Yampa docs. Figuring out exactly which switch I needed was tricky. The Yampa Arcade paper notes that each switch can change how the system behaves, so I hope I picked the right one!

The base switch has a type switch :: SF a (b, Event c) -> (c -> SF a b) -> SF a b. Broken down: SF a (b, Event c) is a signal function that contains an event stream for some type c. An event on this stream will trigger the second argument (the continuation function) c -> SF a b which selects a new signal function for each event. This results in a single signal function that switches behaviour based on the event stream.

A common pattern is to make a recursive call in the second argument. Which we’ll see later.

The problem with the switch type for me is that I didn’t have enough information to create a new signal function in the continuation function. I needed access the current battery state in order to create a new signal function. This requires result of the first signal function to create another signal function. It’s not possible with c -> SF a b. I need something like (b, c) -> SF a b where I have access to the output of the current signal function when creating a new signal function.

The Yampa solution is dkSwitch :: SF a b -> SF (a, b) (Event c) -> (SF a b -> c -> SF a b) -> SF a b. The presence of the second argument (the test function) allows me to pass extra information to the continuation based on the output of the original signal function. Additionally In this version the type c is completely contained in the two inner arguments. This allows me to add parameters without the changing the output signal function. I am not sure if this is a hack or not, but it seemed useful. I chose the type (Control, BatteryState) for c which made the continuation function trivial.

-- continuation recursively calls the battery function with the current state and the new control.
continuation  :: SF (SiteLoad, Event Control) BatteryState -> (Control, BatteryState) -> SF (SiteLoad, Event Control) BatteryState
continuation  _ (newMode, currentState) = battery spec currentState newMode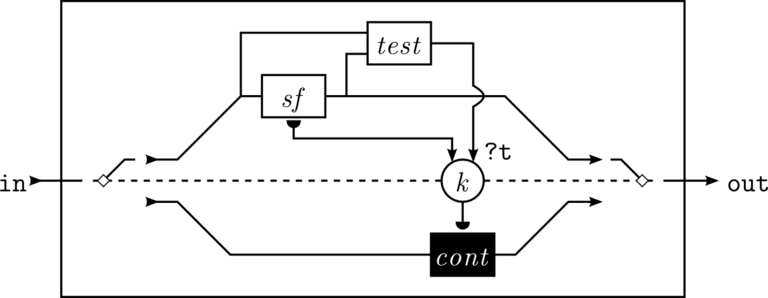

Feedback Loops

Composing the physics with the control logic looks something like this:

fullControl :: SF (BatteryState, SiteLoad) ChargeRequest -> SF (ChangeRequest) BatteryState -> SF (BatteryState, SiteLoad) BatteryState
fullControl control physics = control >>> physics -- almost right

The types almost line up, but we introduce a depenency loop. I want the battery state to disappear from the input to the resulting signal function so I use the loop combinator from the ArrowLoop class.

-- d disappears from the input and output of the original singnal function.
loop :: ArrowLoop a => a (b, d) (c, d) -> a b c

This allows for an output of an arrow to also be fed into its own input. It creates a feedback loop. In my case I created a helper function:

batteryWithControl :: ControlMode -> SF SiteLoad BatteryState

-- and loop specialised to:
loop :: ArrowLoop a => a (SiteLoad, BatteryState) (BatteryState, BatteryState) -> a SiteLoad BatteryState

The type signature also does a good job of describing this. The input and output both contain a d type which is fed back into the input. The resulting arrow has the d type removed from both the input and output. For more about ArrowLoop and feedback loops in Yampa I recommend A New Notation for Arrows by Ross Paterson.

Are we done? notYet.

The biggest problem I had was with switching. The dkSwitch immediately switches to the new signal function defined by the continuation function. This means the first event for the new behaviour is the same event that caused the previous behaviour to switch. This caused my simulation to continuously switch behaviours without making any progress. The Yampa Arcade paper paper has a discussion on this exactly problem, but I didn’t recognise it at the time.

The resulting signal function is composed with notYet :: SF (Event a) (Event a) that suppresses initial event occurrences. Thus the overall result is a source of kill and spawn events that will not have any occurrence at the point in time when it is first activated. This is to prevent gameCore from getting stuck in an infinite loop of switching. The need for this kind of construct typi- cally arises when the source of the switching events simply passes on events received on its input in a recursive setting such as the one above. Since switching takes no time, the new instance of the event source will see the exact same input as the instance of event source that caused the switch, and if that input is the actual switching event, a new switch would be initiated immediately, and so on for ever.

– Yampa Arcade, Section 5.5 Maintaining Dynamic Collections

Composing my test signal function with notYet fixed the problem.

switchDetector :: SF ((SiteLoad, Event Control), BatteryState) (Event (Control, BatteryState))
switchDetector = (arr $ \((_, eMode), state) -> fmap (, state) eMode) >>> notYet

Conclusion

That’s it. I’ll put a full listing of the battery code at the end of this article.

I’m not sure I would use Yampa for small simulations, but for larger simulations with many interacting components the Arrow abstraction is very useful. The ability to track inputs and compose smaller components into larger ones supports my goal of continuing to grow this simulation.

For some reason peripheral subsystems were exceptionally simple to implement. Two examples are plotting charts with gnuplot and building a test harness. The input tracking made building a test harness especially simple and I’m quite pleased with tests like this:

tasty_batteryPhysics :: SignalTest PowerRequest BatteryState
tasty_batteryPhysics = 
  signalTest "charging at 2 kW" testSF (onceAnHourForADay 2.0) $ \result -> do
    it "charges at 2 kW for 4 hours to reach 100% state of charge" $ do
      map soc result `shouldStartWithApprox` [0.5, 0.7, 0.9, 1.0, 1.0]

Likewise charting with gnuplot a breeze.

On the downside, debugging was tricky. And the learning curve for Arrows/Yampa is steep. Furthermore, there are tricks you need to know to use Yampa effectively. The notYet combinator is one example, and I’m a little bit scared there are others I’m not aware of. Similarly the Yampa switches are great, but require some study to understand which one is appropriate for a given situation.

I enjoy working with Arrows, I like being able to compose smaller effectful components into larger ones, and I like the input tracking built into Arrows. For any problem that cannot be represented with pure functions, I would consider using Arrows.

Source Code for the Battery

-- A battery couples local control modes (such as solar soak or load following) with the battery physics.
-- The battery can be set to either of these modes, or to direct charging/discharging/idle modes.
battery :: BatterySpec 
        -> BatteryState 
        -> Control
        -> SF (SiteLoad, Event Control) BatteryState
battery spec initialState initialControl = dkSwitch initialBattery switchDetector continuation
  where
    initialBattery :: SF (SiteLoad, Event Control) BatteryState
    initialBattery = proc (load, _) -> do
      newState <- batteryWithControl (controlFor initialControl) -< load
      returnA -< newState
    
    switchDetector :: SF ((SiteLoad, Event Control), BatteryState) (Event (Control, BatteryState))
    switchDetector = (arr $ \((_, eMode), state) -> fmap (, state) eMode) >>> notYet
    
    continuation  :: SF (SiteLoad, Event Control) BatteryState -> (Control, BatteryState) -> SF (SiteLoad, Event Control) BatteryState
    continuation  _ (newMode, currentState) = battery spec currentState newMode
    
    -- Map Control to ControlMode SF
    controlFor :: Control -> ControlMode
    controlFor SolarSoak = solarSoakControl spec
    controlFor LoadFollowing = loadFollowingControl spec
    controlFor (Charging p) = arr (const p)
    controlFor (Discharging p) = arr (const $ negate p)
    controlFor Idle = arr (const 0)

    -- Battery wraps a control mode signal into a signal that is easier to use with battery physics
    batteryWithControl :: ControlMode -> SF SiteLoad BatteryState
    batteryWithControl controlSF = loop $ proc (load, prevState) -> do
      powerRequest <- controlSF -< (prevState, load)
      newState <- batteryPhysics spec initialState -< powerRequest
      -- iPre delays the state by one time step
      delayedState <- iPre initialState -< newState
      returnA -< (newState, delayedState)